Complete Guide To Understanding Control Charts

What are Control Charts?

Control Charts are a simple yet powerful tool that helps us understand if a process is “stable or in control.” Control Charts are used in the Control phase of the DMAIC (Define, Measure, Analyze, Improve, and Control) process. The charts help us track process statistics over time and help us understand the causes of the variation.

A process can be called stable or under statistical control if it has only one average and one standard deviation. What this means is that the process can still produce materials that are out of specifications. But the deviation is well within a predictable limit, and the whole process is completely under control. The control is specified by a single average, which means that the output quantity remains the same after the whole process is completed.

There are two types of general data: Variable and Attribute.

• Variable data is data that is in a continuum range and can be measured on any scale. For example, height, weight, etc., data can be measured between two numbers on an infinite scale. It is also known as continuous data.
• Attribute data is the type of data that has two types: discrete and numeric. Discrete attribute data assigns a numeric value to a qualitative characteristic of your project. For example, agree, strongly agree, disagree, etc. can be plotted on a scale of 1 to 5, based upon the increasing magnitude of the issue. Numeric attribute data is the type that can be counted. For example, the number of errors in the delivery of a product, customer waiting lines, defects produced in a process, etc.

Why do we need Control Charts?

Control Charts help us identify controlled and uncontrolled variations in a process. Let’s further understand what these variations are and how they affect the process.

Controlled Variation

• They are known as “common causes or inherent (noise) or random causes.” This kind of variation is always present in any kind of process due to the regular and repetitive nature of the input and conversion processes. This variation is natural, and we can never predict the next data point exactly. The common causes will have a brief effect on the process and will appear and disappear randomly, thus awarding it so many names.
• However, if the input and conversion process activities stably repeat themselves, then the common cause variation can be predicted, not accurately, but we can get a range or a band in which the noise variation can take place. A process is considered stable if it has only common causes.

How do we fix it?

• Common causes usually arise from the basics of a process. So, to fix it, fundamental changes are required. Also, there are many strategies to achieve the same goal, like the drill-down strategy, the disaggregate strategy, etc. Thus, as we take these approaches, we can find the noise and reduce or mend it permanently.

Uncontrolled Variation

• They are also called or known as “special cause variables or assignable variables” (signals). This type of variation is not usually present in the input or conversion activity of the process. They originate from outside the process and create changes in the process, making it difficult to identify and analyze common causes.
• Signals affect the natural variation of the process and are the major cause of irregularities or shocks in the process.

How do we fix it?

• You need to work with the data and make sure that the data is accurate and timely. Also, when signals arise, you need to immediately find the cause and fix it. Find or make some changes in the higher-level process to rule out special causes from repeating. And you should never make fundamental changes to fix special causes.

Note: All processes have common causes, but not all processes are affected by special causes.

As previously stated, noise cannot always be avoided because it is a natural variation that we must accept and work with. But signals are more like an anomaly that can point out major flaws in the process and, if fixed, can greatly benefit the entire process.

Types of Control Charts

There are two major types of Control Charts, which are further divided into subcategories, for better understanding the causes, controlling the process, and making it stable or in control. The types of Control Charts are Variable Control Charts and Attribute Control Charts.

Variable Control Charts plot statistics from the measurement data, such as height, length, width, etc.

It is of three types:

• Individual and Moving Range (I-MR)
• X Bar Range Chart (X Bar/ R), X Bar Sample Chart (X-Bar/S)
• 3 Chart I-MR-R (Master Black Belt)

Attributes Control Charts plot a process statistic, which is plotted against a sample number or time.

It is of four types:

• Np-Chart
• P-Chart
• C-Chart
• U-Chart

As we read, there are 7 types of control charts. We will use them as per the data type and then proceed further to get the process stable or in control. Thus, if the data is continuous or variable, we use the I-MR Chart, X-Bar R Chart, and X-Bar S Chart.

If the data is discrete or attribute, then we use P, Np, C, and U Charts.

The charts mentioned below are used for continuous or variable data.

• I – MR Chart
  When we can’t subgroup data, we use the I-MR chart. This measures continuous data, as often we do not get many points, or maybe the process has a long cycle time, so we use this chart. As we learned earlier, there can be data on an infinite scale between two numbers. Thus, this chart proves helpful for plotting this kind of data.
• X-Bar R Chart
  When dealing with continuous data, we have 2 or more, but not more than 10 subgroups. Then we use the X-Bar R chart. This chart helps us determine if a process is stable and predictable. The X represents the mean of all subgroups, and the R represents the range of all subgroups.
• X-Bar S Chart
  When dealing with continuous data, if we have more than 10 subgroups, then we use the X-Bar S chart. We can also use this chart for more than 2 subgroup sizes. The X represents the mean of all subgroups, and the S represents the sample size.

Now let’s move on to discrete data. We use 4 types of charts as discrete or attribute data is divided into 2 parts, i.e., defective items and specific types of defects. So, different charts are used for each use case. The charts mentioned below are used for discrete or attribute data.

Under the category of defective items, we use two types of Control Charts – P and Np.

• P Chart
  The P chart is used to measure and plot the defective discrete data, checking the stability of the process. It plots the number of units that are not fit.
• Np Chart
  The P chart is used to measure and plot the defective discrete data, checking the stability of the process. It plots the proportion of units that are not fit.

Note: The main distinguishing factor between the two is that the P chart is used for varying sample sizes, while the Np chart is used when the sample size is constant.

Under the category of specific defects category, we use two types of Control charts – C and U.

• C chart
  The C chart helps us check the stability of a single unit, which might have one or more defects. For example, the number of defects in one remote. A C-chart plots the number of defects.
• U chart
  The U chart helps us check the stability of a single unit, which might have one or more defects. For example, the number of defects in one remote. A U-chart plots the number of defects per “inspection unit.”

The main distinguishing factor between the two is that the C chart is used when the sample size is fixed, and the U chart is used if the sample size is not fixed. Both charts are used if there is more than one defect.

For a handy approach, use the chart below.

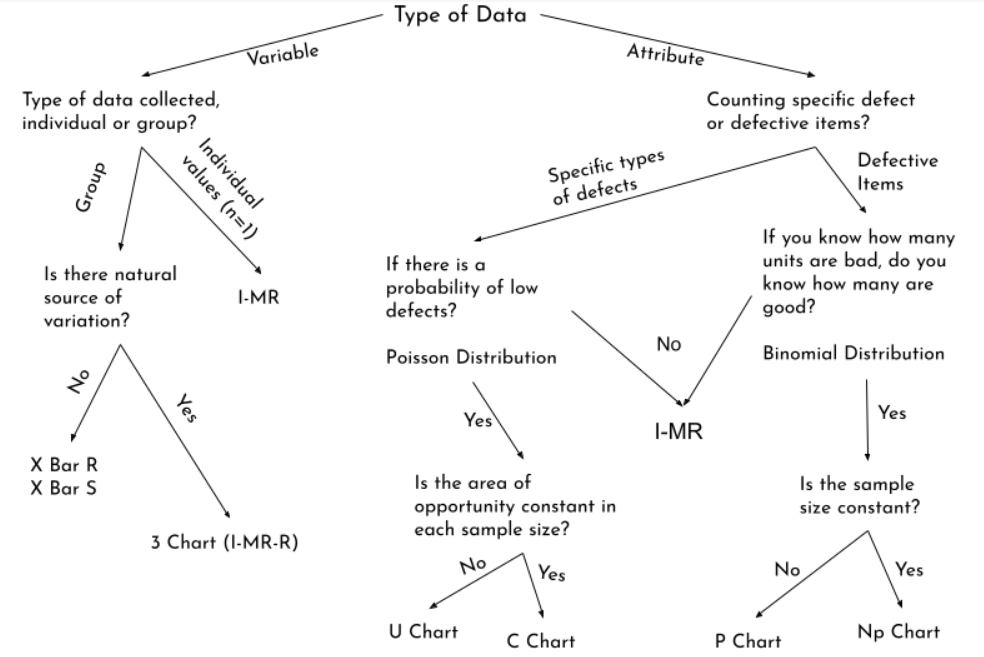
Important points to consider when using Control Charts

• If the value of LCL is negative, assume LCL is 0.
• Because the sample size in the P and U charts varies, we can take the average sample size to obtain a fixed sample.
• Continuous data exhibits two charts, and discrete data exhibits a single chart.
• If the process is in control, it does not mean it’s stable, it just means it is consistent.
• Variable control charts are more sensitive to changes as compared to attribute control charts.
• Variable charts are highly useful for processes such as estimating tool wear and tear.
• Use an individual chart when a few samples are available. This should also be used when the subgroup is not known.
• The U-chart and the C-chart calculate the number of defective units.
• The P-chart and the Np-chart are highly useful for charting proportions.
• Use a U-chart for continuous items, such as fabric, metal sheet, etc.
• C-charts are useful in comparison to U-charts, especially when there are a lot of possible defects, with a small chance of any defect occurring. For example, flaws in a roll of cloth, etc.

Conclusion

In this article, we learned about the importance of Control Charts and how greatly they can benefit the entire process. What must always be kept in mind while using them is to make sure to check and recheck if you are using the right one. Because if you know when to use which control chart, it will not only save you valuable project time but also provide meaningful information and opportunities for improvement in the process.

To conclude, the Control Chart is a boon for process improvement, enabling us to take necessary preventive action for causes that make a process unstable or out of control. A Control chart should be used at time intervals to check the performance of the process. It also works as a health check-up for your process.

In a Lean Six Sigma project, we use a Control Chart at the beginning of the project as well as at the end of the ‘Improve’ phase to implement required changes and keep the process stable or in control.

Original Article: https://6sigma.com/complete-guide-to-understanding-control-charts/